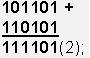4. Интегралните схеми......да ама не.. За съжаление няма да се втурвам много в тази тема. Вместо това ще използвам шанса да придам смисъл на това, което четохте досега и ще ви обясня най-важните елементи на чиповете и тъй като сте вече запознати със начина на интерпретация на данни, пътуващи по електрическите магистрали, ще ви покажа пример с две интегрални схеми свързани по-между си. Разгледайте следната диаграма:
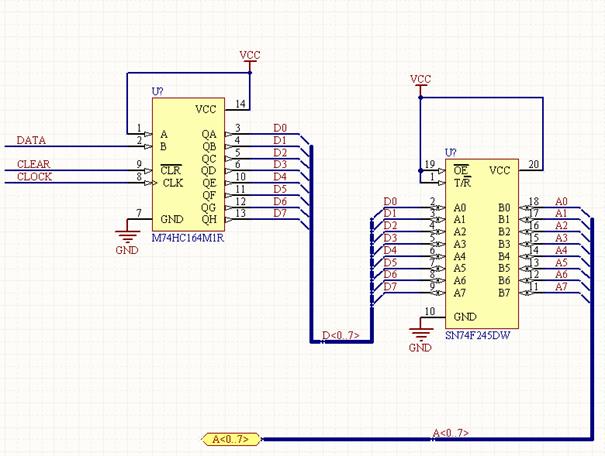
Нека започнем анализа. Първо кои са интегралните схеми? На тази диаграма точно, това са жълтите правоъгълници, с множеството „
крачета” (pin). Тези крачета, всъщност са проводници, част от интегралната схема, които й позволяват да „контактува” със заобикалящия свят. Всеки такъв проводник, има 3 функции –
вход(input ; in),
изход(output ; out) и
захранващи(power). Входовете на цифровите интегрални схеми служат да приемат цифрови сигнали, които променят поведението на интегралната схема по определен начин, зависейки от нивото на сигнала. Примери за входове са A, B, CLR, CLK, OE, T/R и т.н. Изходите на интегрална схема пък, служат да изпращат цифрови сигнали, нивата на които зависят от поведението на схемата. Такива са QA, QB,QC,..Qx от първата инт. схема. Захранващите крачета, както името подсказва, служат да захранват интегралните схеми от право-токов източник. Обикновено се приема символа
GND(земя) за обозначение на крачетата, изискващи захранване от 0V и
Vxx(напрежение) за обозначение на крачета изискващи положително напрежение. Има и крачета които са едновременно входове и изходи, като например схемата от дясно, която има крачета с двупосочни стрелки. Всъщност това не означава, че по един и същи проводник минават сигналите в две посоки едновременно, а че с течение на времето те могат да сменят функциите си от входове на изходи и обратното. И именно това е функцията на тази интегрална схема – да променя посоката на магистралите. Важен елемент който ще забележите, е че повечето крачета са пригодени специално да се свързват с други, обратни на тях по функция чрез електрическа магистрала. Например това са изходите QА - QH от първата нит. схема свързани към входовете A0 – A7 на втората. Всички тези крачета от съответният чип имат една и съща функция и се свързват чрез паралелната магистрала D<0..7>. Така може да се изпрати 8-битово число от първият чип към вторият. Например първата схема може да изпраща числото 45(10) (00101101(2)) към втората. В случая сигналите ще пътуват по съответните линии и състоянията им отдадени от изходите на първата, ще бъдат приети от входовете на втората. Ето най-после един солиден пример за електрическа магистрала в действие. Има още две магистрали – ако забелязвате към входовете B и CLK на първата нит. схема, са свързани две линии DATA и CLOCK, които ако си спомняте са основни елементи на серийна магистрала. Именно този чип, служи да приема данни по серийна магистрала, и да ги изпраща по паралелна. Но как точно, ще се уточни по-нататък.

Третата магистрала A<0..7> е свързана към входо-изходите (I/O) B0 - B7 на втората нит. схема. Всички тези крачета, специално пригодени за връзка чрез електрически магистрали се наричат
портове(port). Сигурно ви е познато това наименование от компютърния хардуер например USB порт, Сериен порт и Паралелния порт. Дотук с интегралните схеми, по-нататък ще разберете повече.
5. Булева алгебраПрез 1854 г. Джордж Бул започва нов раздел от математиката, наречен
булева алгебра. За разлика от нормалната алгебра обаче, тази използва двоичната бройна система, и освен нормалните операции като събиране, изваждане и т.н, се извършват и логически операции върху отделни битове. Тези логически операции са „сърцето” на модерната цифрова електроника, тъй като са основните функции, които извършват най-простите интегрални схеми и които ще разгледаме подробно в следващата тема. Като за начало, нека се запознаем с най-простите, а именно логическо ‘НЕ’, ‘И’ и ‘ИЛИ’.
Логическо ‘
НЕ’ (NOT) или
инвертор(inverter), е най-простата операция, която служи да ‘обръща’ състоянието на даден бит, т.е. истината(true) става неистина(false), 1 става 0, високото ниво става ниско и обратно. В булевата алгебра се използва специален знак - ¬ (или просто -, ~) В електрониката обаче, за да се покаже това състояние (независимо дали е за отделен или много битове/цифрови сигнали) се надчертават имената. Например
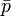
е обратното състояние на ‘р’. За да покажа действието на тази операция, ще използвам т. нар.
таблица на истинността(truth table), която ще използвам всеки път, когато разглеждам операцията на дадено логическо устройство. Нека имаме битовете А и B, като
B = ¬А и получаваме следната таблица за инверсия:
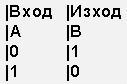
Както виждате, таблицата представлява 2 или повече колони и редове. Всяка колона може да е
входяща(input) или
изходяща(output),т.е. в единия случай се записват текущите състояния на даден бит, а в другия – изходните. На всеки ред се записва комбинацията от битове и изходните им положения. За улеснение, най-често се използват 2 колони, съответно входяща и изходяща, като в всяка се записват под двоично число състоянията на битовете, както ще се убедите по-нататък. Същите тези таблици се използват при анализиране на цифрови у-ва, като А и В са примерно наименованията на входове или изходи. В електрониката или по-точно в електрическите схеми, се използва символът
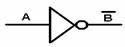
за да илюстрира елементи, които обръщат нивата на ел. сигнали и обикновено този елемент е част от инт. схема. В случая А е вход, а В е изход.
Следващата функция е логическо ‘
И’ (AND ; AND gate), още позната и като логическо умножение или конюнкция. За разлика от логическо ‘НЕ’, тази функция изисква 2 или повече входящи битове, за да се извърши операцията. Означава се със следния знак ‘
∧’ в математиката, в електрониката с ‘
.’ (знак за умножение) и в програмирането и прочие – с ‘
&’. Ще се придържам с означението при електрониката

Ето и таблицата за тази функция, ако имаме
А . B = C:

Както забелязвате единствения случай С да е 1 е когато А и В също са 1, т.е. С е истина ако А и В са истина. Това държание на функцията е много подобно при това на класическото умножение, при което всяко число умножено по 0 е 0, а по 1 дава същото число. В електрониката, елементи използващи електрически нива на сигнали за да се постигне същата функция, се илюстрират със символа
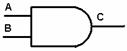
в схемите.
Последната функция логическо ‘
ИЛИ’(OR), логическо събиране или дизюнкция е обратната версия на конюнкцията. Означава се с ‘
∨’ в математиката, ‘
+’ в електрониката и ‘
|’ в програмирането, и както при логическото ‘И’, така и логическото ‘ИЛИ’ изисква 2 или повече операнди. Ето и съответната таблица ако имаме
А + В = С:

Операцията е пълна противоположност на логическото ‘И’ както се забелязва, т.е. единственият момент, в който С е 0 е когато и двата входящи бита също са 0, в всички други комбинации С = 1. Ето как изглежда и съответния елемент в електрониката, извършващ тази функция -
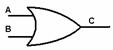
Всички тези операции се прилагат в т.нар. логически уравнения. За да придобиете малка представа за тях и за да опровергая допълнително, че дизюнкцията е действително обратна версия на конюнкцията, нека разгледаме следното уравнение –
¬ (¬А . ¬В) = С <=> ¬А . ¬В = ¬(A + B)Ето как изглежда и таблицата му:

Разглеждайки таблицата и уравнението, лесно се разбира как обръщането на резултата от конюнкция, с обърнати входящи битове става дизюнкция, т.е. ¬ (¬А . ¬В) = С <=> A + B = C. Впрочем представянето на дизюнкцията, чрез конюнкцията в това уравнение е едно от т.нар. логически зависимости или зависимостите на Де Морган. Такава зависимост е и конюнкцията представена чрез дизюнкция –
¬ (¬А + ¬В) = С <=> ¬А + ¬В = ¬(A . B)
И по същия начин, получаваме резултат в последната колона, като този при логическо умножение. Тези уравнения могат да се представят в електрониката по следния начин, чрез респективните символи на операциите във вид на ел. схеми:
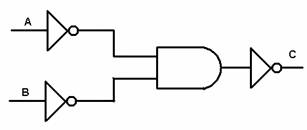 ¬ (¬А . ¬В) = С
¬ (¬А . ¬В) = С 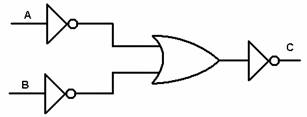 ¬ (¬А + ¬В) = С
¬ (¬А + ¬В) = С Разгледайте ги и разберете как се формират схеми на други уравнения. Други зависимости са например:
A . (B . C) = (A . B) . C;
A + (B + C) = (A + B) + C;
A + (B . C) = (A + B) . (B + C);
A . (B + C) = (A . B) + (B . C);
A + A = A;
A . A = A;
Не бъркаите С от тези уравнения, с С от предишните. В случая това С е вход.Логически операции могат да се извършват не само между отделни битове, а и между цели числа, като за целта се представят в двоичната бройна система и се извършва дадена операция между съответните битове. Ето няколко такива изчисления:
НЕ 68 = ¬ 1000100 = 10111011(2) = 187(10) или
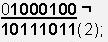
Бележка: При тази операция е задължително да се отбележи максималният брои битове в числото. В случая съм приемаме, че максимума е 8 бита и затова обръщам и нулите в началото на числото(които формално ги няма).
15 И 25 = 1111 . 11001 = 1001(2) = 9(10) или
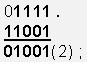
45 ИЛИ 53 = 101101 + 110101 = 111101(2) = 61(10) или